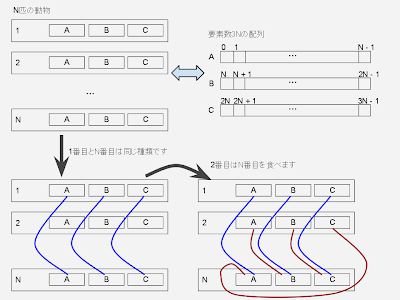
プログラミングコンテストチャレンジブックに載っていた、「食物連鎖」という問題(POJ 1182)。Union-Find木を応用して解けるらしいが、文字の説明だけではすんなり理解できなかったので概念を図にした。すっきりした。
2011年11月20日日曜日
2011年8月16日火曜日
自然対数の底 e の計算 in Elisp
eを計算する方法はたくさんある。ここでは二つの方法を書いておく。
1. 級数
exの x=1 におけるテイラー展開を求めてやると、次のような級数表現が得られる。
この級数表現をプログラムにすると、次のようになる。
(defun e (n)
"級数表現にもとづいてeを計算"
(if (< n 0) 0.0
(+ (/ 1.0 (fact n)) (e (- n 1)))))
=> e
(defun fact (n)
"階乗を計算"
(if (<= n 0) 1
(* n (fact (- n 1)))))
=> fact
(e 5)
=> 2.7166666666666663
n=1 から n=20 までの実行結果。
(2.0 2.5 2.6666666666666665 2.708333333333333 2.7166666666666663 2.7180555555555554 2.7182539682539684 2.71827876984127 2.7182815255731922 2.7182818011463845 2.718281826198493 2.718281808918177 2.7182818042763013 2.7182818091495133 2.718281802164987 2.7182817951863503 2.718281799212947 2.7182818049171673 2.7182818140377822 2.7182818360880554)
プロットしてみた。
2. 一般連分数
具体的な式は、「ネイピア数の表現 - Wikipedia」の「II. 一般連分数による表現」に書いてある。これを漸化式の形で書くと、
1, 2, ... と増えていく部分を i で表すと、
さらに、 j = n - i つまり i = n - j と変換すると、
これをプログラムで表現すると、
(defun e (n)
"一般連分数による表現にもとづいてeを計算"
(labels ((f (j)
(cond
((= n j) (+ 2 (/ 1.0 (f (1- j)))))
((zerop j) n)
(t (+ (- n j) (/ (float (- n j)) (f (1- j))))))))
(f n)))
=> e
(e 5)
=> 2.7184466019417477
※浮動小数点数で計算するために、一箇所だけfloat関数を使っている。
n=1 から n=20 までの実行結果。
(3.0 2.6666666666666665 2.7272727272727275 2.7169811320754715 2.7184466019417477 2.718263331760264 2.71828369389345 2.7182816576664037 2.7182818427778273 2.7182818273518743 2.718281828538486 2.718281828453728 2.7182818284593786 2.7182818284590256 2.7182818284590464 2.718281828459045 2.7182818284590455 2.7182818284590455 2.7182818284590455 2.7182818284590455)
1の方法で求めた図に重ねてプロットしてみた(赤い点)。
2011年8月4日木曜日
オイラー・丸山法とPythonのMatplotlib
MatplotlibはPython向けの2次元プロットライブラリ。Wikipediaの記事「Euler-Maruyama method - Wikipedia, the free encyclopedia」(確率微分方程式の数値解法「オイラー・丸山法」)の、サンプルプログラムの中で使われていたので、インストールすることになった。
以下、Mac OS 10.6.8にMatplotlibをインストールして、Wikipediaのサンプルプログラムを実行したという話。
Matplotlibのインストール
Mac OSの場合、特にMacPortsやHomebrewなどのパッケージ管理ソフトを使っているとインストールがうまくいかないことが多いらしい。というのは、Matplotlibが最新の共有ライブラリにリンクされずに、パッケージ管理ソフトであらかじめ導入されていた別の共有ライブラリにリンクされる、といった現象が起こりやすいから。開発者の人も認識しているようで、README.osxというファイルに"Building mpl on OSX has proven to be a nightmare because of all the different types of zlib, png and freetype that may be on your system."
と書いてあった(まるでナイトメアらしい)。
Mac OS X 10.6.8 (Darwin 10.8.0 x86_64) では、次の手順でインストールができた。
- 1. PythonとNumPyを確認
前提条件として、Python 2.5以上と、NumPyモジュール(version 1.1以上)が必要とのこと。これは以下のコマンドで確認できる。
$ python --version Python 2.6.1 $ python -c "import numpy;print numpy.__version__" 1.2.1
自分で入れたのか最初から入っていたのか記憶が無いが、とりあえず自分の場合はすでに必要なものがインストールされていた。
- 2. githubからMatplotlibを取得
$ git clone https://github.com/matplotlib/matplotlib.git
- 3. make.osxの一部を書きかえる
$ cd matplotlib $ vi make.osx $ git diff make.osx diff --git a/make.osx b/make.osx index 4639eac..8dc60c7 100644 --- a/make.osx +++ b/make.osx @@ -3,6 +3,7 @@ # make -f make.osx PREFIX=/Users/jdhunter/dev PYVERSION=2.6 fetch deps mpl_install # (see README.osx for more details) +PREFIX=/usr/local MPLVERSION=1.1.0 PYVERSION=2.6 PYTHON=python${PYVERSION} @@ -16,8 +17,8 @@ ARCH_FLAGS=-arch i386 -arch x86_64 # but the download URLs are subject to change. ZLIBVERSION=1.2.5 -PNGVERSION=1.5.1 -FREETYPEVERSION=2.4.4 +PNGVERSION=1.5.4 +FREETYPEVERSION=2.4.6変更点は3つ。第一に、共有ライブラリのインストールパスを"/usr/local/lib"にしたいので、
PREFIX=/usr/localを追加。それから、libpng と freetype のバージョンを現時点で最新の番号にした。- 4. makeする
-
$ make -f make.osx fetch deps mpl_install_std
これを実行すると、
fetch, deps, mpl_install_stdという3つのターゲットが処理される。fetchがzlib等のライブラリのソースをダウンロードしてきて、depsがライブラリのコンパイルとインストールをして、最後にmpl_install_stdがMatplotlib自身のコンパイルとインストールを行う流れ。完了したら、
/usr/local/libと/Library/Python/2.6/site-packages/matplotlibを確認してみる。$ ls -t1 /usr/local/lib/ libz.1.2.5.dylib libz.1.dylib (略) $ ls -t1 /Library/Python/2.6/site-packages/matplotlib mlab.pyc mpl.pycf offsetbox.pyc (略) $ otool -L /Library/Python/2.6/site-packages/matplotlib/_png.so /Library/Python/2.6/site-packages/matplotlib/_png.so: /usr/local/lib/libpng15.15.dylib (compatibility version 20.0.0, current version 20.0.0) /usr/local/lib/libz.1.dylib (compatibility version 1.0.0, current version 1.2.5) /usr/lib/libstdc++.6.dylib (compatibility version 7.0.0, current version 7.9.0) /usr/lib/libSystem.B.dylib (compatibility version 1.0.0, current version 125.2.0)
ポイントは(1)共有ライブラリができていて、(2)matplotlibのモジュールができていて、(3)モジュール内の共有ライブラリが(1)の共有ライブラリに依存していることの3つ。
オイラー・丸山法
常微分方程式の世界における「オイラー法」に対応するのが「オイラー・丸山法」らしい。「丸山」のフルネームは丸山儀四郎。
Euler-Maruyama method - Wikipedia, the free encyclopedia のExample code(Python)をそのままコピー&実行するとグラフができる。
コードでrandomとか使ってるからあたり前だけど、「実行する度に結果が変わってOK」という考えが新鮮。これまで確定的な微分方程式の数値計算しか扱ったことが無かったので変な感じがする。
ざっと検索したところ、普通のプログラミング環境ではなくエクセルを使って計算する人もいる(そういう方向性の本が出版されている)。
2011年7月25日月曜日
二分ヒープ in Elisp(かなり妥協)
ヒープソートで使う二分ヒープ(binary heap)。副作用を使わないリスト版を作ろうと思ったが、いいアイデアがない。
結局、よくある配列版のアルゴリズムで妥協した…
;;; すみませんがトップレベルの変数を使いますよ、と
(defvar *heap*)
=> *heap*
(defvar *n*)
=> *n*
;;; 初期化関数
(defun init-heap (N)
(setf *heap* (make-vector N -1) *n* 0)
N)
=> init-heap
;;; 追加する関数(最小値が根になるよう並べる)
(defun heap-push (x)
(let ((i *n*) (i-parent))
(incf *n*)
;; 親と比べながら上へ移動
(while (and (> i 0)
(< x (elt *heap* (setf i-parent (/ (- i 1) 2)))))
(aset *heap* i (elt *heap* i-parent))
(setf i i-parent))
(aset *heap* i x)))
=> heap-push
;;; 取り出す関数
(defun heap-pop ()
(if (zerop *n*)
nil
(let ((ret (elt *heap* 0))
(i 0)
(i-child nil)
(v-child nil)
(v-last (elt *heap* (1- *n*))))
;; 子と比べながら下へ移動
(while (and (setf i-child (select-child-idx i))
(< (setf v-child (elt *heap* i-child)) v-last))
(aset *heap* i v-child)
(setf i i-child))
(aset *heap* i v-last)
(decf *n*)
ret)))
=> heap-pop
;;; 補助関数(i番目の要素の子を求める。子が2つある場合は値が小さいほうを選ぶ)
(defun select-child-idx (i)
(let ((cleft (+ (* 2 i) 1))
(cright (+ (* 2 i) 2)))
(cond ((and (< cright *n*)
(< (elt *heap* cright) (elt *heap* cleft)))
cright)
((< cleft *n*) cleft)
(t nil))))
=> select-child-idx
やっぱりElispで配列を扱うのはめんどくさい。変数のsetf, asetが本当につらい…
続いて動作確認。
;;; 10要素のヒープを作る (init-heap 10) => 10 ;; 乱数10個作って push する (mapcar 'heap-push (loop for i from 1 to 10 collect (random 100))) => (29 80 21 8 70 96 19 93 62 86) ;; 10回ぶん pop してみる (loop for i from 1 to 10 collect (heap-pop)) => (8 19 21 29 62 70 80 86 93 96)
ちゃんと小さい順に pop されているのでOKだが、もっときれいに書きたい。
Wikipediaの二分ヒープのページを見てたら「スレッド木」というキーワードが載っていたので今度調べる。あるいは "Purely Functional Data Structures" とかか。
2011年7月1日金曜日
sleep sort in Elisp
いまさらながら "sleep sort" というネタを知った。非同期処理を使ったすごい発想。
いちおうElispで書いてみた。run-at-timeなんて関数があるんですねー、と。
(defun sleep-sort (lat)
(if (null lat) nil
(lexical-let ((n (car lat)))
(run-at-time n nil (lambda () (print n))))
(sleep-sort (cdr lat))))
(sleep-sort '(3 2 1 0))
2011年6月25日土曜日
重複組み合わせ(個数に制限がある場合) in Elisp
「重複組合せ」より引用:
n 種のものから r 個取り出す組合せ(並べ方)の総数を求めよ。
ただし、同種のもの同士に区別はなく、それぞれ a1、a2、a3、・・・、an 個ずつ存在し、 n=a1+a2+a3+・・・+an≧r とする。
要するに、卑近な例を挙げれば「靴下どれでも5足で1,000円。ただしどれも在庫わずか」みたいな状況における、組み合わせの数でしょうか。こういう数のことを一般的に重複組合せ(ちょうふくくみあわせ、repeated combination)と呼び、個数の制限が無い場合は nHm=m+n-1Cm = m+n-1Cn-1 で計算することができるとのこと(数学で習ったかもしれないけど、nHmなんて記号は覚えていない)。
以下では、個数制限ありの場合の問題を解くプログラムを書いてみた。n種類の物が並んでいる中から、(a)先頭の物を1個取り出す場合、(b)取り出さない場合、のそれぞれについて関数を再帰的に適用して、和を取っていけばいいだけ。
;;; lat: 個数のリスト(a1, a2, ..., an)
;;; r: 取り出す数
(defun solve (lat r)
(cond
((null lat) 0) ;リストが空なので 0
((zerop r) 1) ;最後まで取り出したので 1
(t (+ (if (<= 1 (car lat)) ;先頭の物を取り出す場合
(solve
(cons (1- (car lat)) (cdr lat)) ;先頭の物を1個消費
(1- r)) ;あと r - 1 個取り出す必要がある
0) ;在庫切れで取り出せないから 0
(solve (cdr lat) r))))) ;先頭の物を取り出さない場合
;;; テスト
(solve '(1) 1)
=> 1
(solve '(1 1 1) 1)
=> 3
;; 以下の3通り
;; 1 0 0
;; 0 1 0
;; 0 0 1
(solve '(2 2 2) 3)
=> 7
;; 以下の7通り
;; 2 1 0
;; 2 0 1
;; 1 2 0
;; 1 1 1
;; 1 0 2
;; 0 2 1
;; 0 1 2
(solve '(10 10 10) 10)
=> 66
最後の 66 の信憑性に関しては、こちらのページ「重複組み合わせ」に、3種類のものが10個ずつある中から10個とる場合の数は 66 だと書いてあったので間違いないと思われる。
ここでは自然に再帰で考えたけれども、漸化式を導出して動的計画法を使うと O(n×r) で解ける。具体的な方法は「Amazon.co.jp: プログラミングコンテストチャレンジブック: 秋葉 拓哉, 岩田 陽一, 北川 宜稔: 本」に書いてある。式の展開が多少面倒かもしれないが、紙と鉛筆を用意して臨めば問題ないレベルだった(数学嫌いでなければ)。
分割数 in Elisp
いわゆる「組み合わせ数学」の問題。整数 n を m 以下の整数の和で表す方法が何通りあるかを求めるというもの。考え方は「動的計画法」が参考になる。
単なる再帰で解く
(defun partition-num (n m)
(cond
((or (= n 0) (= m 1)) 1)
(t (+ (if (>= n m) (partition-num (- n m) m) 0)
(partition-num n (1- m))))))
=> partition-num
(partition-num 3 3)
=> 3
(partition-num 4 3)
=> 4
(partition-num 9 9)
=> 30
動的計画法的に配列を使って解く
my-make-arrayという関数で多次元配列とそのアクセサみたいな関数を作っている。要するに、Emacs Lisp で多次元配列を使うのは面倒くさいということ。
;;; 多次元配列と、その要素を読み書きする関数(ref, set)を作る関数
;;; 内部的にはデータを1次元配列でもつ。クロージャと連想配列でできている。
(defun my-make-array (&rest dim)
(lexical-let ((dim dim) (v (make-vector (apply '* dim) 0)))
(flet ((index (args) (cond
((null dim) 0)
(t (+ (* (apply '* (cdr dim)) (car idx))
(index (cdr dim) (cdr idx)))))))
`((ref ,(lambda (&rest args) (elt v (index dim args))))
(set ,(lambda (val &rest args) (aset v (index dim args) val)))))))
=> my-make-array
;;; 関数を適用する関数
(defun my-call (obj method &rest args)
(apply (second (assoc method obj)) args))
=> my-call
;;; 配列を使って分割数を解く関数
(defun partition-num-dp (n m)
(let ((dp (my-make-array (1+ n) (1+ m))))
(loop for i from 0 to n do
(loop for j from 1 to m do
(my-call dp 'set i j
(if (or (<= j 1) (zerop i)) 1
(+ (my-call dp 'ref i (1- j))
(if (>= i j)
(my-call dp 'ref (- i j) j)
0))))))
(my-call dp 'ref n m)))
(partition-num-dp 4 3)
=> 4
(partition-num-dp 9 9)
=> 30
2011年6月13日月曜日
最長増加部分列の長さ in Elisp
最長増加部分列(Longest Increasing Subsequence, LIS)の長さを求める問題を、Lisp風に解いただけ。
とりあえず手を動かして例題を解いてみる
これも動的計画法の有名な問題なので、漸化式で考える方法が普通かもしれない。が、自分の場合は例題を手作業で解いているときに頭の中で行っている計算をプログラムに書き直した感じなので、再帰的な解法になっている(空リストのときはゼロ、要素1個のリストの場合は1を返すという前提で開始すれば自然に再帰的な思考になる、はず)。
例題としては Wikipediaに載っていたもの (0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15) を考える。この数列のLISはユニークではなく (0, 2, 6, 9, 13, 15) と (0, 4, 6, 9, 11, 15) の二種類あり、LISの長さは 6。
;; 最後の要素から順番に、各要素を先頭とするLIS長を求めていく。 ;; 計算を具体的に手でやってみると、次のような流れになる(リストに作用させる関数をfとおく)。 (f 15) => 1 (f 7 15) => 2 ;7 < 15 なので (f 15) + 1 => 1 + 1 (f 11 7 15) => 2 ;11 < 15 なので (f 15) + 1 => 1 + 1 (f 3 11 7 15) => 3 ;3より大きい11,7,15で始まるLISはそれぞれ長さが2,2,1。maxの2に1加えて3 (f 13 3 11 7 15) => 2 ;13 < 15 なので (f 15) + 1 => 1 + 1 (f 5 13 3 11 7 15) => 3 ;5より大きい13か11か7で始まるLISが最長で2。それに1加えて3 (f 9 5 13 3 11 7 15) => 3 ;9より大きい13か11で始まるLISが最長で2。それに1加えて3 (f 1 9 5 13 3 11 7 15) => 4 ;1より大きい9や5で始まるLISが最長で3。それに1加えて4 (f 14 1 9 5 13 3 11 7 15) => 2 ;14 < 15 なので (f 15) + 1 => 1 + 1 (f 6 14 1 9 5 13 3 11 7 15) => 4 ;6より大きい数のうち、9で始まるLISが最長で3。それに1加えて4 (f 10 6 14 ...略) => 3 ;10より大きい11,13のLISが最長で2。それに1加えて3 (f 2 10 6 ...略) => 5 ;2より大きい6のLISが最長で4。それに1加えて5 (f 12 2 10 ...略) => 3 ;12より大きい13, 14のLISが最長で4。それに1加えて3 (f 4 12 2 ...略) => 5 ;5より大きい数のうち、6で始まるLISが最長で4。それに1加えて5 (f 8 4 12 ...略) => 4 ;8より大きい12,10,9のLISが最長で3。それに1加えて4 (f 0 8 4 ...略) => 6 ;0より大きい数のうち、2で始まるLISが最長で5。それに1加えて6
Elispで
上で書いた解法をEmacs Lisp化する。使っている組み込み関数はcond, null, or, max, apply, mapcar, remove-if-not。remove-if-notで全てremoveされてしまう場合に備え、orを使って空リストのリスト'(())を返すところが今ひとつだがしょうがない。また、補助関数のsublistsというのはたとえば(1 2 3)を((1 2 3) (2 3) (3))のような形、つまり各要素を先頭とするリストのリストに変換するためのもの。これも別の形できれいに書けそうだが今は思いつかない。
(defun lis-length (lst)
(cond
((null lst) 0) ;空リストなら0
(t (1+ ;サブ問題を解いて、その中の最大値に1を足す
(apply 'max
(mapcar
'lis-length
(or
(remove-if-not ;先頭の数より大きい数から始まるリストだけ抽出
(lambda (sublst) (> (car sublst) (car lst)))
(sublists (cdr lst))) ;先頭の数を除いたリスト全て
'(()))))))))
=> lis-length
(defun sublists (lst)
(cond
((null lst) nil)
(t (cons lst (sublists (cdr lst))))))
=> sublists
;;; テスト
(sublists '(1 2 3))
=> ((1 2 3) (2 3) (3))
(lis-length nil)
=> 0
(lis-length '(15))
=> 1
(lis-length '(7 15))
=> 2
(lis-length '(11 7 15))
=> 2
(lis-length '(0 8 4 12 2 10 6 14 1 9 5 13 3 11 7 15))
=> 6
あとはこの関数にメモ化の機能を追加してやれば、性能が上がって動的計画法で解いたのと同じになる(はず)。
2011年6月7日火曜日
個数制限つき部分和問題 in Elisp
プログラミングコンテストチャレンジブック演習「個数制限付き部分和問題」 - 日々精進に問題文が載っている。これも動的計画法の問題。
とりあえず性能を考えずに書いてみた場合
再帰で自然に書ける。
;;; 個数制限つき部分和問題
;;; - 数と個数のリスト ((数 個数) (数 個数) (数 個数) ...)
;;; - 総和 K
;;; を与える。総和Kを満たす組合せが存在する場合は t を、その他の場合は nil を返す。
(defun solve (lst K)
(cond
((zerop K) t) ;ちょうどゼロ => t
((< K 0) nil) ;マイナス => 解なし
((null lst) nil) ;もう追加できない => 解なし
(t (or
(if (< 0 (cadar lst)) ;数を追加できる(0個以上ある)
(solve (decrease-first-num lst) (- K (caar lst))))
(solve (cdr lst) K))))) ;次の数を試す
=> solve
;;; 補助関数
(defun decrease-first-num (lst)
(cons (list (caar lst) (1- ( cadar lst))) (cdr lst)))
=> decrease-first-num
;;; 補助関数の動作確認
(decrease-first-num '((1 4) (2 2) (3 3)))
=> ((1 3) (2 2) (3 3))
;;; 動作確認
(solve '((3 3) (5 2) (8 2)) 17)
=> t
(solve '((3 3) (5 2) (8 2)) 15)
=> nil
性能改善版(動的計画法あるいはメモ化)による
まず、関数solveの引数が取り得る範囲を減らすため、数の「個数」の部分を1ずつ減らしたりせず固定する。すると第一引数のlstを最大n種類になるので、第二引数のKと合わせて最大 n * K の組み合わせで全ての引数が表現でき、メモ化などで計算量を抑えることができる。その代わり関数の戻り値を t, nil の2値ではなく整数にして、リストの先頭の数が何個余るかを表すようにする(Kになる組み合わせがないときは -1 で表す)。
とりあえず数が1種類の場合と空リストの場合だけ考えると、
(defun solve* (lst K)
(cond
((null lst) -1) ;空リストなら解なし
((zerop K) (second (car lst))) ;K=0なら数を1個も消費しないので、個数をそのまま返す
((< K (first (car lst))) -1) ;数が大き過ぎるなら解なし
((and (<= (first (car lst)) K) ;Kから数を引くことができる?
(< 0 (solve* lst (- K (first (car lst)))))) ;Kから数を1個引いた場合の問題を解いたら、まだ数が余る?
(1- (solve* lst (- K (first (car lst)))))) ;余った数から1を引くと、解になる
(t -1))) ;その他の場合は解けない
=> solve*
;;; テスト
(solve* '() 2)
=> -1
(solve* '((2 1)) 1)
=> -1
(solve* '((2 1)) 2)
=> 0 ;解あり
(solve* '((2 1)) 3)
=> -1
この発想になれたら、数が何種類もある場合も考慮する。先頭の要素をスキップしても解けたという場合を追加するだけなのであまり変わらないが、次のようになる。
(defun solve* (lst K)
(cond
((null lst) -1) ;空リストなら解なし
((or (zerop K) ;K=0?
(<= 0 (solve* (cdr lst) K))) ;現在の数をスキップして解いたら、解けた?
(second (car lst))) ;現在の数を1個も消費しないので、個数をそのまま返す
((< K (first (car lst))) -1) ;数が大き過ぎるなら解なし
((and (<= (first (car lst)) K) ;Kから数を引くことができる?
(< 0 (solve* lst (- K (first (car lst)))))) ;Kから数を1個引いた場合の問題を解いたら、まだ数が余る?
(1- (solve* lst (- K (first (car lst)))))) ;余った数から1を引くと、解になる
(t -1))) ;その他の場合は解けない
=> solve*
;;; テスト
(solve* '((2 2) (4 2) (6 2) (8 2)) 40)
=> 0 ;解あり
(solve* '((2 2) (4 2) (6 2) (8 2)) 39)
=> -1
あとは、例によってこの再帰的関数をメモ化するとよい。
2011年6月6日月曜日
0-1ナップサック問題その2(重さWが巨大な場合) in Elisp
プログラミングコンテストチャレンジブック演習「ナップサック問題その2」 - 日々精進にも書いてある、動的計画法の問題。重さの総和Wが非常に大きい場合、重さを変数とする漸化式で n * W のテーブルを作ると計算量の制限を越えてしまうことがある。そういう場合は発想を変えて、価値を変数とする漸化式を考えよう、という話。すると、計算量は
と表されるようになり、巨大な W の値に依存しなくなる。
コード(Elisp)
配列は使わず、メモ化再帰で作る(メモ化の機能は後で付加する)。
solve-with-knapsack*がお膳立てをしてから、再帰的関数knapsack*を実行する。knapsack*が全て実行し終わると、再びsolve-with-knapsack*のほうが結果を整理して、最終的な解を出す。
;; 価値 v を満たす最小の重さを求める関数。
;; 解が無い場合は異常値(999999)を返す。
(defun knapsack* (lst v)
(cond
;; v がゼロでないということは、解なし
((null lst) (if (zerop v) 0 999999))
;; 品物の価値が大き過ぎる場合
((< v (cadar lst)) (knapsack* (cdr lst) v))
;; 品物を入れない場合と入れる場合を試し、軽いほうを採用
(t (min
(knapsack* (cdr lst) v)
(+ (caar lst) (knapsack* (cdr lst) (- v (cadar lst))))))))
knapsack*
;;; ちょっと確認
(knapsack* '((10 1) (15 2) (30 3)) 0)
=> 0
(knapsack* '((10 1) (15 2) (30 3)) 3)
=> 25
(knapsack* '((10 1) (15 2) (30 3)) 7)
=> 999999
;;; knapsack* を利用して問題を解く関数
(defun solve-with-knapsack* (lst w)
(apply 'max ;価値が最大のものを選択
(mapcar 'car ;価値だけを抽出
(remove-if ;重過ぎる結果は削除
(lambda (x) (> (cdr x) w))
(mapcar
;; (0 1 2 ... Sum vi)を満たす重さを求めて、(価値 . 重さ) のドット対にする
(lambda (v) (cons v (knapsack* lst v)))
;; 0 から 価値の総和までの数列(0 1 2 ... Sum vi)
(loop
for i from 0 to (apply '+ (mapcar 'second lst))
collect i))))))
=> solve-with-knapsack*
;;; 確認
(solve-with-knapsack* '((50 1) (40 2) (30 3) (20 4) (10 5)) 60)
=> 12
実行時間をざっと調べる
;;; 計測するための関数
(defun profile (func &rest args)
(let ((start (current-time)))
(apply func args)
(time-to-seconds (time-subtract (current-time) start))))
=> profile
;;; 重さと価値のリストを乱数で作り *lst* という変数に入れる
(defun gen-lst (n)
(setf *lst*
(loop for i from 1 to n collect (list (random 1000) (random 10)))))
=> gen-lst
;;; リストの要素数 n と実行時間の関係をざっと見る。Wは1000で固定。
;;; まだ再帰的関数をメモ化していないので、 2のn乗で増えていく。
(gen-lst 12)
=> ((801 6) (262 7) (923 5) (131 6) (221 0) (520 5) (221 9) (41 5) (209 6) (743 2) (791 2) (583 0))
(profile 'solve-with-knapsack* *lst* 1000)
=> 0.247282
(gen-lst 13)
=> ((977 2) (756 1) (256 3) (628 9) (743 2) (497 3) (551 0) (101 1) (51 4) (882 6) (181 4) (492 6) (649 4))
(profile 'solve-with-knapsack* *lst* 1000)
=> 0.451455
(gen-lst 14)
=> ((387 5) (154 5) (316 1) (803 0) (330 0) (450 9) (41 1) (257 5) (550 8) (575 6) (988 6) (69 8) (294 2) (330 7))
(profile 'solve-with-knapsack* *lst* 1000)
=> 1.229625
;;; 以下はメモ化した場合。nに対して鈍感になる。
(defun memo (fn name key test)
"Return a memo-function of fn."
(lexical-let ((_fn fn) (_key key) (table (make-hash-table :test test)))
;(setf (get name 'memo) table)
#'(lambda (&rest args)
(let ((k (funcall _key args)))
(if (gethash k table)
(gethash k table)
(setf (gethash k table) (apply _fn args)))))))
=> memo
(defun* memoize (fn-name &key (key #'first) (test #'eql))
"Replace fn-name's global definition with a memoized version."
(setf (symbol-function fn-name)
(memo (symbol-function fn-name) fn-name key test)))
=> memoize
(memoize 'knapsack* :key 'identity :test 'equal)
=> (lambda (&rest --cl-rest--) (apply (lambda (G6503 G6504 G6505 &rest args) (let ... ...)) (quote --table--) (quote --_key--) (quote --_fn--) --cl-rest--))
(gen-lst 14)
=> ((909 9) (234 2) (563 3) (890 8) (520 6) (951 8) (754 4) (810 7) (596 0) (334 1) (876 9) (799 8) (537 8) (735 8))
(profile 'solve-with-knapsack* *lst* 1000)
=> 0.011307
(gen-lst 15)
=> ((557 5) (365 2) (66 2) (794 7) (616 2) (9 1) (237 7) (364 2) (405 6) (976 5) (356 2) (558 7) (224 7) (876 0) (348 6))
(profile 'solve-with-knapsack* *lst* 1000)
=> 0.010048
2011年5月31日火曜日
個数制限なしナップサック問題 in Elisp
ナップサック問題の基本形には「n種類の品物が1個ずつ」という条件が付いていた。よって、この条件を無くした問題を考えよう、という話が自然に出てくる。
条件の有無を区別するため、前者を「0-1ナップサック問題」、後者を「個数制限なしナップサック問題」とか "UKP: unbounded knapsack problem" と呼ぶのが一般的らしい。
何も考えないで入力を与えると両者の違いが現れないこともあるが、たとえば (重さ, 価値) のリストが((2 2) (3 4) (5 7))、重さの制限W=9 と与えると次のように出力に違いが出てくる。
- 0-1ナップサック問題の場合
- 答え 11 … (3 4) と (5 7) の要素を選択するので 4 + 7 で 11
- 個数制限なしナップサック問題の場合
- 答え 12 … (3 4) の要素を3個選択するので 4 × 3 で 12
以下、個数制限なしのほうを解くプログラムを考える。と言っても 0-1ナップサック問題を再帰的に解いている場合は少し変更するだけで個数制限なしのほうも解ける。
;; 0-1ナップサック問題
(defun knapsack (lst w)
(cond
((null lst) 0)
(t (if (> (caar lst) w) ;先頭の品物が入らない場合
(knapsack (cdr lst) w)
(max ;入れる場合と入れない場合を両方とも試し、良い結果のほうを選ぶ
(+ (cadar lst) (knapsack (cdr lst) (- w (caar lst))))
(knapsack (cdr lst) w))))))
上のプログラムの後半部分((max)の中)で、先頭の品物を何度も入れるようにする。具体的には、
(max ;入れる場合と入れない場合を両方とも試し、良い結果のほうを選ぶ
(+ (cadar lst) (knapsack (cdr lst) (- w (caar lst))))
(knapsack (cdr lst) w))))))
を次のように変える。
(max ;先頭の品物を繰り返し入れる場合と、入れない場合を試して良いほうを選ぶ
(+ (cadar lst) (knapsack lst (- w (caar lst))))
(knapsack (cdr lst) w))))))
要するに (cdr lst)をlstに変え、コメントを編集しただけ。
最後に確認。
(defun knapsack (lst w)
(cond
((null lst) 0)
(t (if (> (caar lst) w) ;先頭の品物が入らない場合
(knapsack (cdr lst) w)
(max ;先頭の品物を繰り返し入れる場合と、入れない場合を試して良いほうを選ぶ
(+ (cadar lst) (knapsack lst (- w (caar lst))))
(knapsack (cdr lst) w))))))
=> knapsack
(knapsack '((2 2) (3 4) (5 7)) 9)
=> 12
この関数の引数を眺めてみると、最大で n × W 種類しかないことが自然に分かる。つまり個数制限無しの場合も、0-1の場合と同じく n × W のメモ化テーブルに結果を保持することで計算量を減らせる。
2011年5月26日木曜日
メモ化再帰: symbol-function を使う方法
Elispで再帰的関数をメモ化する方法の続き。
Y Combinator による方法のほかにも、symbol-function を使って関数定義を書き換える方法がある。
symbol-functionを使ったメモ化再帰の例(Elisp)
(defun memo (fn name key test)
"Return a memo-function of fn."
(lexical-let ((_fn fn) (_key key) (table (make-hash-table :test test)))
#'(lambda (&rest args)
(let ((k (funcall _key args)))
(if (gethash k table)
(gethash k table)
(setf (gethash k table) (apply _fn args)))))))
=> memo
(defun* memoize (fn-name &key (key #'first) (test #'eql))
"Replace fn-name's global definition with a memoized version."
(setf (symbol-function fn-name)
(memo (symbol-function fn-name) fn-name key test)))
=> memoize
;;; フィボナッチ数列で試す
(defun fib (n)
(if (<= n 1) 1
(+ (fib (- n 1)) (fib (- n 2)))))
=> fib
;;; 実行時間をはかる関数
(defun profile (func &rest args)
(let ((start (current-time)))
(apply func args)
(time-to-seconds (time-subtract (current-time) start))))
-> profile
;;; メモ化なしの場合の実行時間
(profile 'fib 25)
=> 0.124392
;;; fibをメモ化する
(memoize 'fib)
=> (lambda (&rest --cl-rest--) (apply (lambda (G90287 G90288 G90289 &rest args) (let ... ...)) (quote --table--) (quote --_key--) (quote --_fn--) --cl-rest--))
;;; メモ化した場合の実行時間
(profile 'fib 25)
=> 0.000166
ちなみにこの方法は、"Paradigms of Artificial Intelligence Programming" というCommon Lispの本に載っていた(9.1 Caching Results of Previous Computations: Memoization)。そのプログラムを、 defun*, lexical-let等を利用してEmacs Lisp 用に調整しただけ。
2011年5月25日水曜日
Longest Common Subsequence の長さ in Elisp
Common Subsequence 解説 や、 最長共通部分列問題 (Longest Common Subsequence) - naoyaのはてなダイアリー で紹介されている問題。動的計画法やメモ化で計算量が減らせる例として知られている、とのこと。
(defun lcs-length (l1 l2)
(cond
((or (null l1) (null l2)) 0)
((eq (car l1) (car l2))
(+ (lcs-length (cdr l1) (cdr l2)) 1))
(t
(max
(lcs-length l1 (cdr l2))
(lcs-length (cdr l1) l2)))))
=> lcs-length
(lcs-length '(a b c b d a b) '(b d c a b a))
=> 4
2011年5月24日火曜日
ナップサック問題とメモ化 in Elisp
有名なナップサック問題を Emacs Lisp で勉強である。
ナップサック問題とは「重さと価値がそれぞれ wi, vi, である品物から、重さの総和が W を超えないように選んだときの、価値の総和の最大値を求める」問題である。
素朴なバージョン
価値の最大値を求める関数を作る。入力は ((w1, v1) (w2, v2) ... (wn, vn)) なる形のリストと、総和 W の2つ。
(defun knapsack (lst w)
(cond
((null lst) 0)
(t (if (> (caar lst) w) ;先頭の品物が入らない場合
(knapsack (cdr lst) w)
(max ;入れる場合と入れない場合を両方とも試し、良い結果のほうを選ぶ
(+ (cadar lst) (knapsack (cdr lst) (- w (caar lst))))
(knapsack (cdr lst) w))))))
;; 確認
(knapsack '((10 7) (4 2) (5 9) (1 4) (7 9) (3 7) (6 4) (3 5)) 20)
=> 34
n個の品物それぞれについて、入れる/入れないの二通りを計算する考え方であり、最大計算量は O(2n) となる。
※確認には ナップサック問題とは? に載っている例を使っている。
※Emacs のバージョンは GNU Emacs 22.3.1
メモ化(memoization)を行うバージョン
上の関数 knapsack が再帰的に実行されるときの引数を分析すると、第一引数は長さnのリストから先頭の要素が一つずつ取り去られていくので合計 n種類になる。また、第二引数は初期値 W から何らかの整数を引いた値であるから、最大で W - 1 から 0 までの整数の数、つまりW種類になる。
第一引数が n 通りで第二引数が W 通りなので、引数の場合の数は結局のところ n * W 通り。メモ化を利用して n * W程度の領域に結果を保存すれば、最大計算量を 2n から n * W のオーダーに減らすことができるわけである。
次に、具体的にどうやってメモ化を行うかを考える。素朴な方法は、グローバル変数としてハッシュテーブルを定義しておき、knapsackの中でそれを参照するというもの。しかし、この方法は関数をグローバル変数に依存した形に書き換えなければならず、再利用やコピペがしにくくなる。
そこで、もう少し独立性を保てるよう、Yコンビネータを利用した方法を使う。この方法については、 さあ、Yコンビネータ(不動点演算子)を使おう! - よくわかりません を参考に、YコンビネータのコードはY combinator - Rosetta Code の中のCommon Lispバージョンを参考にするとよい(Elispでも動くように let ではなく lexical-let を使った形に書き換えるなどする)。
;; メモ化機能を組み込んだ Y です
(defun Y (f)
(lexical-let ((_f f) (cache (make-hash-table :test #'equal)))
((lambda (x) (funcall x x))
(lambda (y)
(lexical-let ((_y y))
(funcall _f (lambda (&rest args)
(if (gethash args cache)
(gethash args cache)
(setf (gethash args cache)
(apply (funcall _y _y) args))))))))))
;; Yコンビネータ向けに、ラムダ式を返す形
(defun knapsack-memo (f)
(lexical-let ((_f f))
(lambda (lst w)
(cond
((null lst) 0)
(t (if (> (caar lst) w)
(funcall _f (cdr lst) w)
(max
(+ (cadar lst) (funcall _f (cdr lst) (- w (caar lst))))
(funcall _f (cdr lst) w))))))))
;; 確認
(funcall
(Y 'knapsack-memo)
'((10 7) (4 2) (5 9) (1 4) (7 9) (3 7) (6 4) (3 5)) 20)
=> 34
以下は、計算時間を比較した例。
;; 時間をざっと計る関数
(defun profile (func &rest args)
(let ((start (current-time)))
(apply func args)
(time-to-seconds (time-subtract (current-time) start))))
=> profile
;; 重さと価値のリスト
(setq *w-v-list* '((10 7) (4 2) (5 9) (1 4) (7 9) (3 7) (6 4) (3 5) (3 5) (5 3) (1 2) (3 4) (1 5) (2 2) (4 5) (2 2) (4 5) (3 9) (1 5)))
=> ((10 7) (4 2) (5 9) (1 4) (7 9) (3 7) (6 4) (3 5) (3 5) (5 3) (1 2) (3 4) ...)
;; 素朴なバージョンは約 0.43 秒
(profile 'knapsack *w-v-list* 30)
=> 0.438918
;; メモ化バージョンは約 0.06 秒
(profile (Y 'knapsack-memo) *w-v-list* 30)
=> 0.063991
n をもっと増やすと劇的に差が出るはず。ちなみに手軽に時間を計る関数は実行時間の測定 どう書く?org から流用したもの。
2011年5月22日日曜日
ハフマン符号 in Elisp
ハフマン符号化法のプログラムは「計算機プログラムの構造と解釈」(SICP)を参考にするとよい。完全な形では載っていないので、演習問題をいくつか解く必要はあるが。
概要
任意の文字列をハフマン符号化法によって符号化したり復号化したりしたい。これに必要になる関数は、大雑把に挙げると次の4つ。
- ハフマン木を作る関数(文字と頻度の組の集合を入力 ⇒ ハフマン木を出力)
- 符号化する関数(符号化したい文字列とハフマン木を入力 ⇒ 符号を出力)
- 復号化する関数(符号とハフマン木を入力 ⇒ 元の文字列を出力)
- 文字列内の文字の出現頻度を求める関数
以下、それぞれのコードをEmacs lispで書いていく。
ハフマン木を作る関数
データ構造はSICPに書かれているとおりで、木と葉の二種類を組み合わせてハフマン木を構成する。
木のほうは、
- 左のノード
- 右のノード
- 文字の集合
- 頻度の合計値
…の合計4要素。葉のほうは、
- 葉であることを表すシンボル
leaf - 文字
- 文字の頻度
木は関数 make-code-tree で、葉は関数 make-leaf で生成する。そのほかに、木/葉に含まれる文字の集合を集める関数 symbols や頻度の合計を求める関数 weight 等を書いたのが以下のコード。
(defun make-leaf (symbol weight)
(list 'leaf symbol weight))
(defun leafp (object)
(eq (car object) 'leaf))
(defun symbol-leaf (x)
(cadr x))
(defun weight-leaf (x)
(caddr x))
(defun symbols (tree)
(if (leafp tree)
(list (symbol-leaf tree))
(caddr tree)))
(defun weight (tree)
(if (leafp tree)
(weight-leaf tree)
(cadddr tree)))
(defun make-code-tree (left right)
(list left
right
(append (symbols left) (symbols right))
(+ (weight left) (weight right))))
;; ちょっと確認
(make-code-tree (make-leaf 'b 1) (make-leaf 'c 2))
=> ((leaf b 1) (leaf c 2) (b c) 3)
続いて、 ((c 3) (b 2) (a 1)) のような形で文字と出現頻度の組が与えられると、それをハフマン木に変換する関数 generate-huffman-tree を書く。ここで、make-leaf-set が ((c 3) (b 2) (a 1)) の各要素を葉に変換しつつ adjoin-set を利用して頻度の昇順に並べかえ、successive-merge は昇順のリストから先頭の葉/木を2つ取り出して、つまり貪欲法的に選択して、木を構成していく関数。
(defun generate-huffman-tree (pairs)
(successive-merge (make-leaf-set pairs)))
(defun adjoin-set (x set)
(cond ((null set) (list x))
((< (weight x) (weight (car set))) (cons x set))
(t (cons (car set)
(adjoin-set x (cdr set))))))
;; ちょっと確認
(adjoin-set (make-leaf 'a 4)
(list (make-code-tree (make-leaf 'b 2) (make-leaf 'c 1))))
=> (((leaf b 2) (leaf c 1) (b c) 3)
(leaf a 4))
(defun make-leaf-set (pairs)
(if (null pairs)
'()
(let ((pair (car pairs)))
(adjoin-set (make-leaf (car pair) ; symbol
(cadr pair)) ; frequency
(make-leaf-set (cdr pairs))))))
;; ちょっと確認
(make-leaf-set '((c 3) (b 2) (a 1)))
=> ((leaf a 1)
(leaf b 2)
(leaf c 3))
(defun successive-merge (set)
(cond ((null set) '())
((= (length set) 1) (car set))
(t (successive-merge
(adjoin-set (make-code-tree (car set) (cadr set))
(cddr set))))))
;; ハフマン木を生成して確認
(generate-huffman-tree
'((e 5) (d 4) (c 3) (b 2) (a 1)))
=> (((leaf c 3)
((leaf a 1)
(leaf b 2)
(a b)
3)
(c a b)
6)
((leaf d 4)
(leaf e 5)
(d e)
9)
(c a b d e)
15)
;; 木を図にしてみると、問題なさそう
15
6 9
3 3 4 5
1 2
符号化する関数(符号化したい文字列とハフマン木を入力 ⇒ 符号を出力)
encode という関数を作る。符号化したい文字列は、(A D A B B C A) のようなリストの形で与え、一文字を符号化する関数 encode-symbol を補助関数として使用する。そうすると、コードは次のようになる。
(defun encode (message tree)
(if (null message)
'()
(append (encode-symbol (car message) tree)
(encode (cdr message) tree))))
(defun encode-symbol (symbol tree)
(if (member symbol (symbols tree))
(cond ((leafp tree) nil)
((member symbol (symbols (left-branch tree)))
(cons 0 (encode-symbol symbol (left-branch tree))))
(t (cons 1 (encode-symbol symbol (right-branch tree)))))
(error "the symbol %S doesn't exist in the tree -- ENCODE-SYMBOL" symbol)))
;; ハフマン木を仮に定義して確認
(setq *my-test-tree*
(make-code-tree (make-leaf 'A 4)
(make-code-tree
(make-leaf 'B 2)
(make-code-tree (make-leaf 'D 1)
(make-leaf 'C 1) ))))
=> ((leaf A 4) ((leaf B 2) ((leaf D 1) (leaf C 1) (D C) 2) (B D C) 4) (A B D C) 8)
(encode-symbol 'A *my-test-tree*)
=> (0)
(encode-symbol 'D *my-test-tree*)
=> (1 1 0)
(encode-symbol 'E *my-test-tree*)
=> error
(encode '(A D A B C) *my-test-tree*)
=> (0 1 1 0 0 1 0 1 1 1)
復号化する関数(符号とハフマン木を入力 ⇒ 元の文字列を出力)
decode 関数を作る。符号は、(0 1 1 0 0 1 0 1 1 1) のようなゼロと1のリストで、出力も(A D A B C)のようなリスト。メインの decode は、flet で定義した補助関数 decode-1 を呼び出す形。ビットを先頭から取りだして木を探索し、葉に到達したらその葉が持つ文字を自然なる再帰にcons する。そのほかに、left-branch, right-branch, choose-branch も定義。
(defun decode (bits tree)
(flet ((decode-1
(bits current-branch)
(if (null bits)
'()
(let ((next-branch (choose-branch
(car bits)
current-branch)))
(if (leafp next-branch)
(cons (symbol-leaf next-branch)
(decode-1 (cdr bits) tree))
(decode-1 (cdr bits) next-branch))))))
(decode-1 bits tree)))
(defun left-branch (tree) (car tree))
(defun right-branch (tree) (cadr tree))
(defun choose-branch (bit branch)
(cond ((= bit 0) (left-branch branch))
((= bit 1) (right-branch branch))
(t (error "bad bit %S -- CHOOSE-BRANCH" bit))))
;; 既出の例で確認
(decode '(0 1 1 0 0 1 0 1 1 1) *my-test-tree*)
=> (A D A B C)
文字列内の文字の出現頻度を求める関数
最後に、文字列を調査して文字と頻度のリストを生成する関数count-occurences を作る。これの出力を上述のgenerate-huffman-tree に渡すことになる。
概要としては、loopマクロで文字と頻度から成る連想リスト(association list)を作っておき、mapcarによってドット対をリストに変換する、という流れになっている。
(defun count-occurences (str)
(let ((n (length str)) tbl)
(loop for i from 0 to (1- n) do
(if (assoc (elt str i) tbl)
(incf (cdr (assoc (elt str i) tbl)))
(setf tbl (cons (cons (elt str i) 1) tbl))))
(mapcar (lambda (x)
(list (car x) (cdr x))) tbl)))
;; 確認(文字コード 97 が a に対応)
(count-occurences "aaa bb c")
=> ((99 1) (98 2) (32 2) (97 3))
統合
最終確認。
;; 文字列
(setq *my-message* "BACADAEAFABBAAAGAH")
=> "BACADAEAFABBAAAGAH"
;; 文字列からHuffman木を作る
(setq *my-h-tree* (generate-huffman-tree
(count-occurences *my-message*)))
=> ((leaf 65 9) (((... ... ... 2) (... ... ... 2) (67 68 69 70) 4) ((... ... ... 2) (leaf 66 3) (71 72 66) 5) (67 68 69 70 71 72 66) 9) (65 67 68 69 70 71 72 66) 18)
;; 符号化(string-to-list で文字列を文字のリストに変換している)
(setq *my-encoded-message*
(encode (string-to-list *my-message*) *my-h-tree*))
=> (1 1 1 0 1 0 0 0 0 1 0 0 ...)
;; ビット長さ
(length *my-encoded-message*)
=> 42
;; 復号化(string をapply して文字のリストを文字列に変換)
(apply 'string (decode *my-encoded-message* *my-h-tree*))
=> "BACADAEAFABBAAAGAH"
以上、貪欲法の例としてのハフマン符号化。とても素朴な実装と思われる(性能等を考えると改善の余地がたくさんある)。
2011年5月17日火曜日
柵の修理問題 Fence Repair Problem
3253 -- Fence Repairという問題をやってみるテスト。
- 問題
- 農家のJohnが農場の柵を修繕しようと計画したところ、L1, L2, ..., LNの長さをもつN枚の板が必要だと分かった。
彼は、L1からLNまでの総和に等しい長さの板を一枚買い、それをノコギリで切り分けることにした。
しかし、ノコギリを持っていないことに気づいたので、知りあいの農家Donにノコギリを貸してくれるよう打診した。
資本家でもあるDonはノコギリを貸さず、自分が板を切る作業をN-1回行う代わりに各回ごとに料金を請求したいと提案した。各回の料金とは、そのときに切断する板の長さと同じ。すなわち、長さ21の板を板に切り分ける場合は21となる。
この料金の考え方に従うと、板を切る順番によって最終的な請求額が変化する。Johnが支払うべき最小の金額を求めよ。
解くための考え方
例として長さ 21 の板から長さ 8, 5, 8 の3つの板に分ける場合を考えると、次の二通りの分け方がある。
- まず 13 と 8 に分け、次に長さ 13 の板を 8 と 5 に分ける。
- まず 16 と 5 に分け、次に長さ 16 の板を 8 と 8 に分ける。
これを図示したのが次の図。1番目の料金が 21 + 13 = 34 となり、2番目は 21 + 16 = 37 となるので、1番目のほうが安く上がる。
大雑把な分析だが、図はデータ構造で言うところの二分木の形になり、木の下のほうに短い板があったほうが全体のコストが小さくなる。したがって、問題を解くためには、N枚の板の中からできるだけ短い板を集めながらボトムアップに木を構築していけばよい。その様子を示したのが下図。
短い板を優先して集めるので、これも「貪欲法」のアルゴリズムと言える。また、木の構成方法が「ハフマン符号化法」で使う「ハフマン木」と同じになっている。ただし、この問題ではコストの合計値が分かればよいので、木を完全に構成する必要はない。
コードと実行例(Emacs Lisp で)
入力として L1, L2, ..., LN をリストで渡すと、結果(最小の料金)を返すような関数にした。
(defun fence-repair (lst)
"メインの関数です"
(cond
((null lst) 0)
((= (length lst) 2) (apply '+ lst))
(t
(multiple-value-bind (pos-min pos-next-min)
(position-smallest-two lst)
(let ((sum (+ (nth pos-min lst) (nth pos-next-min lst))))
(+ sum
(fence-repair
(remove-nth
pos-min
(replace lst (list sum) :start1 pos-next-min) ))))))))
(defun remove-nth (n list)
"リストからn番目の要素を消す"
(if (zerop n)
(cdr list)
(cons (car list) (remove-nth (1- n) (cdr list)))))
(defun position-smallest-two (list)
"最小値をもつ要素と、2番目に小さい値をもつ要素の位置を返す"
(let* ((min 0) (next-min 1) (n (length list)) (i 1))
(while (< i n)
(cond
((< (nth i list) (nth min list))
(setf next-min min) (setf min i) )
((< (nth i list) (nth next-min list))
(setf next-min i) ))
(incf i) )
(list min next-min) ))
以下は実行例で、それぞれ (8, 5, 8) と (1 1 2 2 3 3) の場合。
(fence-repair '(8 5 8))
=> 34
(fence-repair '(1 1 2 2 3 3))
=> 30
;;おそらく以下のような二分木になるはず (+ 12 7 5 4 2) で 30
12
7 5
4 3 2 3
2 2
1 1
今度はハフマン符号化のプログラムをELispで作ってみたい。SICPにヒントが載ってるし。
2011年4月28日木曜日
硬貨の組み合わせ問題(貪欲法の簡単な例題)
貪欲法や欲張り法(greedy algorithm, greedy strategy)と呼ばれるアルゴリズムの話。
このアルゴリムのよく知られた例は、ある金額を実現する硬貨の組合せの中で枚数が最も少ないものを求める問題。たとえば「765円のお釣を払う場合、500円硬貨1枚、100円硬貨2枚、50円硬貨1枚、10円硬貨1枚、5円硬貨1枚の計6枚」という結果は「高額の硬貨から順番に使って払う」ことによって求まる。「高い硬貨から使っていくという点で『欲張り』」らしい。
とても分かりやすいアルゴリズムである反面、局所的に最善の選択を繰り返すに過ぎないので、条件次第では最適解が求まらないこともある。
以下はこの問題を解く具体的な例だが、1円玉から500円玉のそれぞれについて枚数に制限を加えた形になっている。また、Elispなので金額と枚数の組を表すのに連想リスト(association list)を使っている。
;;; 引数は、金額と、利用可能な硬貨を表す連想リスト(金額と枚数)
(defun solve (yen coins)
(if (zerop yen) nil
(let ((n (min (/ yen (caar coins))
(cdar coins) )))
(cons (cons (caar coins) n)
(solve (- yen (* n (caar coins)))
(cdr coins) )))))
;;; 例1.
;;; 金額: 765円、
;;; 使える硬貨: 500円*1、100円*1、50円*3、10円*3、5円*3、1円*3
(solve 765 '((500 . 1) (100 . 1) (50 . 3) (10 . 3) (5 . 3) (1 . 3)))
=> ((500 . 1) (100 . 1) (50 . 3) (10 . 1) (5 . 1))
;;; 例2.
;;; 金額: 623円、
;;; 使える硬貨: 500円*0、100円*5、50円*3、10円*1、5円*2、1円*5
(solve 623 '((500 . 0) (100 . 5) (50 . 3) (10 . 1) (5 . 2) (1 . 10)))
=> ((500 . 0) (100 . 5) (50 . 2) (10 . 1) (5 . 2) (1 . 3))
2011年4月15日金曜日
順列を求めるプログラム(Perl、Elisp)
"Higher-Order Perl" という本を読む。順列を求めるプログラムが載っている。何かの役にたつかもしれないから覚えとこう、と思い実際に書いてみる。ついでにEmacs Lispでも書いてみる。
Perlで順列(permutation)を求める
Higher-Order Perl: - Google ブックス より、そのまま引用。
sub permute{
my @items = @{ $_[0] };
my @perms = @{ $_[1] };
unless(@items){
print "@perms\n";
} else {
my(@newitems, @newperms, $i);
foreach $i (0 .. $#items) {
@newitems = @items;
@newperms = @perms;
unshift(@newperms, splice(@newitems, $i, 1));
permute([@newitems], [@newperms]);
}
}
}
# sample call:
permute([qw(red yellow blue green)], []);
"permute.pl"というファイルに保存し、実行してみる。
$ perl ./permute.pl green blue yellow red blue green yellow red green yellow blue red yellow green blue red blue yellow green red yellow blue green red green blue red yellow blue green red yellow green red blue yellow red green blue yellow blue red green yellow red blue green yellow green yellow red blue yellow green red blue green red yellow blue red green yellow blue yellow red green blue red yellow green blue blue yellow red green yellow blue red green blue red yellow green red blue yellow green yellow red blue green red yellow blue green
順序が反対になって出力されるのが気になるが(red yellow blue green が最初に出力されて欲しい)、これはunshiftをpushに変えれば済む話なのでよしとする。
Emacs Lispの場合
loopは使わずに、マップ関数で実現。
(defun permute (lat)
(cond
((null lat) '(()))
(t (mapcan
(lambda (atm)
(mapcar (lambda (lst) (cons atm lst))
(permute (remove* atm lat :count 1))))
lat))))
Perlよりだいぶすっきり。しかし一つひとつの関数が濃い。
実行結果。
(permute '(red yellow blue green))
=> ((red yellow blue green) (red yellow green blue)
(red blue yellow green) (red blue green yellow)
(red green yellow blue) (red green blue yellow)
(yellow red blue green) (yellow red green blue)
(yellow blue red green) (yellow blue green red)
(yellow green red blue) (yellow green blue red)
(blue red yellow green) (blue red green yellow)
(blue yellow red green) (blue yellow green red)
(blue green red yellow) (blue green yellow red)
(green red yellow blue) (green red blue yellow)
(green yellow red blue) (green yellow blue red)
(green blue red yellow) (green blue yellow red))
導出について
上記の関数を作るときの考え方を書いておく。
まず、具体的な計算例を想像して分析してみる。たとえば3要素のリスト (a b c) に対して期待される結果は ((a b c) (a c b) (b a c) (b c a) (c a b) (c b a)) となる。
このうち、最初の2つの部分リスト ((a b c) (a c b)) は、 a を リスト (b c) と (c b) に cons した形なので次式で表せる。
(mapcar (lambda (lst) (cons 'a lst)) '((b c) (c b)))
さらに、第二引数の((b c) (c b))は、(b c)の順列だから、(permute '(b c))と表せる。
(mapcar (lambda (lst) (cons 'a lst)) (permute '(b c)))
残り4つの部分リストも同様に(mapcar (lambda ...) (permute ...))の形で表し、これらを連結(nconc)する。
(nconc (mapcar (lambda (lst) (cons 'a lst)) (permute '(b c))) (mapcar (lambda (lst) (cons 'b lst)) (permute '(a c))) (mapcar (lambda (lst) (cons 'c lst)) (permute '(a b))))
同じようなコードの重複を無くすため、mapcanを使って変形する。
(mapcan
(lambda (atm)
(mapcar (lambda (lst) (cons atm lst))
(permute (remove* atm '(a b c) :count 1))))
'(a b c))
remove*は第1引数と等しい要素を第2引数からすべて削除する関数だが、キーワードパラメータとして :count 1 を指定すれば削除する個数を制限できる。
この段階で再帰的関数の主要部分ができたので、(a b c)を関数の引数 lat として defun に変換する。
(defun permute (lat)
(cond
((null lat) ???)
(t (mapcan
(lambda (atm)
(mapcar (lambda (lst) (cons atm lst))
(permute (remove* atm lat :count 1))))
lat))))
あとは保留してある「???」の部分、すなわち再帰が終了する場合の式を考えれば完成。
そのため、要素1個のリスト (a) の順列を求める過程を具体的にトレースしてみる。
(permute '(a))
;; cond の t に対応する式
=> (mapcan
(lambda (atm)
(mapcar (lambda (lst) (cons atm lst))
(permute (remove* atm '(a) :count 1))))
'(a))
;; mapcan を評価して、atm を 'a に置換
=> (nconc
(mapcar (lambda (lst) (cons 'a lst))
(permute (remove* 'a '(a) :count 1))))
;; remove* と nconc を評価(引数が1個なので nconc は実質的に何もしない)
=> (mapcar (lambda (lst) (cons 'a lst))
(permute nil))
ここまで展開すると、(a)の順列を求めた結果が ((a)) となるためには(permute nil) の結果が (()) であればよいということがきっと分かる。
(mapcar (lambda (lst) (cons 'a lst))
'(()))
=> ((a))
よって、保留した部分も '(()) と書けばよい。これでようやく関数が完成。
(defun permute (lat)
(cond
((null lat) '(()))
(t (mapcan
(lambda (atm)
(mapcar (lambda (lst) (cons atm lst))
(permute (remove* atm lat :count 1))))
lat))))
2011年4月10日日曜日
Emacs Lisp で迷路の最短路問題(最小のターン数を求める)
深さ優先探索アルゴリズムと同じく初期状態からたどり着ける全ての状態を探索するが、初期状態に近い状態から順番に探索するので最短経路が確実に求まる。
例題:迷路の最短路(経路は求めずに距離だけ)
- 問題
- 通路と壁からできている迷路があり、1ターンに隣接する上下左右4マスの通路(いわゆる「4近傍」)へ移動できる。スタートからゴールまで移動するのに必要な最小のターン数を求める(ただし、スタートからゴールまで移動できると仮定)。
- 迷路の例
....####..####.#...# .#.##.......#.#..... .#S#...#.##.#.#..##. .###....#..##....#.# ........####..#####. ##.#..#.#....#.#..#. .#.###..#.#.##..#.#. ...#.#....#.##..###. #..#...#.####G.##.#. ...#.#.#......#...## ##...#.....###.#.#.# #.#..#####.#...####. ###....###.##.###.##
ここで、 S, G, ., # はそれぞれスタート、ゴール、通路、壁を表す。
解(Emacs Lispの場合)
一般的な解法では、迷路と同じサイズの二次元配列を最初に用意しておき、探索をしながらスタート地点からのターン数、すなわち距離の値を配列に記録していく。また、二次元配列を初期化するときに特異な値を代入することで、その座標が探索済みかどうか判断できるようにしておく。この解法を踏まえつつ、次の変更を加えてEmacs Lispで実装した。
- 二次元配列は使わず、探索済みの座標をリストに記録していく
- 探索済み座標のリストには、ターン数もセットで記録する。要素は、行・列・ターン数の3要素をもつリストになるので、たとえば '((0 1 1) (1 0 1) (0 2 2) (1 2 2) ...) というような形になる
- 迷路の座標と一対一に対応する配列を持たないので経路を求めることはできないが、ターン数だけを求めるのでこれでよしとする
;;; 幅優先探索(BFS)の例題:迷路の最短路問題
(defun minimum-distance ()
"カーソルを迷路の下に移動させて実行すると、スタート(S)とゴール(G)の距離をミニバッファに出力。探索した場所を / に置換しながら進む。"
(interactive)
(save-excursion
(search-backward "S")
(let* ((flg t) ;発見したらnil
(dist 0) ;距離
(visited) ;探索済み座標のリスト
(queue (list-next-positions dist))) ;探索する座標のリスト
(while (and queue flg) ;探索対象あり、かつ未発見の場合
(funcall ;queueからpopした要素に関数を適用
(lambda (pos) ;ゴールか調べつつ、queueに追加
(progn
(goto-line (first pos))
(move-to-column (second pos))
(sit-for 0.05)
(cond
((eq (char-after) ?G) ;ゴールかどうか
(message "Answer: %d" (third pos)) ;結果表示
(setf flg nil)) ;while終了
(t (insert ?/)
(delete-char 1)
(backward-char)
(setf queue ;次の探索対象をqueueに追加
(append
queue
(list-next-positions (third pos)) ))))))
(pop queue) )))))
(defun list-next-positions (dist)
"現在のカーソル位置から次の探索位置を求める補助関数。結果はリストにして返す。また、動的スコープを利用してminimum-distance の中の visited も変更する。"
(let* ((row (line-number-at-pos))
(col (current-column))
(poslist `((,(1- row) ,col) ;移動方向 上
(,row ,(1+ col)) ;右
(,(1+ row) ,col) ;下
(,row ,(1- col))))) ;左
(setf visited ;呼び出し元の visited を変更
(mapcar
(lambda (pos) (append pos `(,(1+ dist)))) ;距離を追加
(remove-if
(lambda (pos)
(let ((row (first pos))
(col (second pos)) )
(or (< col 0) ;列がマイナスの場所は対象外
(progn (goto-line (first pos)) ;通路かゴール以外は対象外
(move-to-column (second pos))
(not (find (char-after) '(?. ?G))))
(some (lambda (v) ;探索済みなら対象外
(and (eq row (first v)) (eq col (second v))))
visited))))
poslist)))))
実行&結果
- *scratch*バッファなどで、".", "#", "S", "G" を使った迷路のASCIIアートを描く(SからGまで辿り着けるようになっていること)。
- M-x minimum-distance を実行する。
- 通路"."が"/"に置換されていき、"G"に逹するとミニバッファにターン数が表示される。
2011年3月29日火曜日
Emacs Lisp で Lake Counting
コード
vector型(いわゆる配列)は使わない方針。つまり、配列にデータを読み込んで添字でアクセスするのではなく、Emacsのバッファに記述されている文字列をそのまま処理する。したがって、"point"関連の組み込み関数を多用している。また、8近傍の要素を表す一時的なデータも、配列ではなくリストにしている。
(defun lake-count (b e)
"入力となるリージョンを選択した状態で M-x lake-count を実行すると、答えをミニバッファに出力する。"
(interactive "r")
(save-excursion
(let ((cnt 0)
(first-line (line-number-at-pos b)) ;リージョンの先頭行番号を記録しておく
(last-line (line-number-at-pos e))) ;リージョンの最終行番号を 〃
(loop for p from b to e do
(goto-char p)
(sit-for 0.1) ;カーソルの動きを観察するため一瞬停止
(when (eq ?W (char-after p))
(dfs)
(incf cnt) ))
(message "%d" cnt)))) ;結果出力
(defun dfs ()
"補助関数。現在のポイントを文字.に置換する。8近傍に文字Wがあれば再帰的に適用する。"
(let* ((cline (line-number-at-pos))
(ccol (current-column))
(poslist `((,(1- cline) ,(1- ccol)) ;8近傍を表す(行,列)のリスト
(,(1- cline) ,ccol)
(,(1- cline) ,(1+ ccol))
(,cline ,(1- ccol))
(,cline ,(1+ ccol))
(,(1+ cline) ,(1- ccol))
(,(1+ cline) ,ccol)
(,(1+ cline) ,(1+ ccol)) )))
(delete-char 1) ; この2行で W を . に置換
(insert ?.) ; 〃
(setf poslist
(remove-if ;リージョンの外に出る要素をリストから消す
(lambda (pos)
(or (< (first pos) first-line);上にはみ出す場合
(> (first pos) last-line) ;下にはみ出す場合
(< (second pos) 0))) ;左にはみ出す場合
poslist))
(mapcar (lambda (pos) ;8近傍の各要素に対してラムダ式を適用
(goto-line(first pos))
(move-to-column (second pos)) ;近傍にポイントを移動
(sit-for 0.1) ;カーソルの動きを観察するため一瞬停止
(if (eq ?W (char-after)) ;Wなら再帰的に呼び出す
(dfs)))
poslist)))
使用している組み込み関数/マクロ
詳細はEmacs上でdescribe-functionを行えば出てくるので、列挙だけしておく。
- let
- let*
- loop
- when
- incf
- eq
- sit-for
- insert
- delete-char
- mapcar
- remove-if
- char-after
- goto-line
- move-to-column
- mapcar
- save-excursion
- goto-char
- first
- second
よいか悪いかは別として、C言語などで書く場合と比べると、たくさんの語彙を駆使したプログラムになってしまう(バッククォートとか、カンマまで使っている…)。
実行&結果
- *scratch*バッファなどで、"W"と"."を使った水たまりのASCIIアートを描く。
- 先頭の行をC-SPCでマークして、カーソルを最後の行まで移動。全体を選択状態にする。
- M-x lake-count を実行する。
- 最終的にすべての"W"が"."に置換され、ミニバッファに水たまりの数が表示される。
W........WW. .WWW.....WWW ....WW...WW. .........WW. .........W.. ..W......W.. .W.W.....WW. W.W.W.....W. .W.W......W. ..W.......W.上記の入力の場合、正解は 3。動画も作ってみたが、全画面表示にしないと見えない。